Pietro Rainero
Lagunando 2024 > AUTORI 2024

Pietro Rainero
Laureato in fisica con una tesi sui quark ed è da poco tempo in pensione dopo essere stato docente di matematica e fisica in diversi licei.
Collabora con riviste e siti web e scrive anche per l’importante e seguitissimo blog culturale ”Alla volta di Leucade”.
Dal 2013 è giurato nella sezione racconti del premio “Gozzano” e dal 2022 è presidente di Giuria nella sezione fiabe del concorso “Città di Cologna Spiaggia”.
Ha scritto 137 racconti, è presente su 318 antologie e ha pubblicato dodici raccolte di racconti.
Ha al suo attivo anche una settantina di primi posti nei concorsi di prosa. Ama misurarsi con una grande varietà di temi all’insegna dell’ironia, dell’antifrasi, della leggerezza, del gusto contaminatorio, di un estro talora surreale.
“Orti dei Dogi”
Narrativa
MANDORLI GIAPPONESI
“Professore, professor Coleman!” gridò Takami-musubi.
Sidney Coleman si voltò alla sua destra, vide il cartello che Takami-musubi teneva ben in vista con le braccia tese in alto e pensò Ah, eccolo il mio accompagnatore.
Si diresse verso chi lo aveva chiamato, facendo scorrere con la mano sinistra il trolley sul pavimento.
“Piacere” disse Coleman.
“Piacere, professore. Mi chiamo Takami-musubi e sono l’incaricato di scortarla fino a Itsukushima, per il congresso”
“Ottimo, mi faccia strada”
Questo scambio di battute si svolse, cari lettori, nella sala d’arrivo dell’enorme aeroporto Haneda di Tokio, dove Sidney Coleman era appena atterrato a bordo di un Boeing 747 proveniente da Los Angeles. Dagli Stati Uniti, sì, perché Coleman insegnava ad Harvard.
E forse a voi non dirà nulla, ma Sidney Coleman, pur non essendo noto al grande pubblico e non avendo nessuna visibilità all’esterno della comunità dei fisici teorici, all’interno della stessa comunità era una specie di dio maggiore: lui era il fisico dei fisici.
Si racconta che, un giorno, arrivando in ritardo ad una riunione di colleghi e intuendo dalla porta d’entrata della stanza del convegno che si stava dibattendo una questione particolarmente spinosa, avesse fatto irruzione esclamando “Ce l’ho io la soluzione! Qual è il problema?”.
A Itsukushima, località situata sull’isola di Miyajima, vicino ad Hiroshima e sede di uno spettacolare santuario shintoista, si teneva in quel periodo di primavera l’annuale riunione dei fisici teorici, quella volta dedicata ai recenti progressi nei calcoli di elettrodinamica quantistica.
E Takami-musubi, di due anni più giovane dell’illustre scienziato, aveva il compito di accompagnarlo su di un aereo delle linee nazionali da Tokio fin sull’isola di Miyajima, e poi fino all’albergo sede quell’anno del convegno dei fisici, convegno dedicato a Hideki Yukawa, colui che aveva predetto l’esistenza dei mesoni pi greco, i pioni.
Prendiamo dunque posto anche noi, cari lettori, sull’aereo in partenza da Tokio (il biglietto ve lo offro io) e andiamo ad origliare il dialogo tra i due.
“Mi dica, Takami, lei è sposato?”
“Sì, sono sposato con Hanako Izumi e ho due figli, Kunihiko e Fuyuko. Il maschio ha 34 anni e lavora come ingegnere presso una centrale elettrica mentre la femmina studia ancora”
“E cosa studia?”
“Matematica. Lei sarà contento!”
“Ah, certo. Un ingegnere e una matematica. A proposito, lei conosce quella barzelletta dell’ingegnere, del fisico e del matematico?”
“No”
“Dunque, ci sono un ingegnere, un fisico e un matematico su di un aereo che sta sorvolando la Scozia, quando dall’oblò scorgono una pecora nera. “Ah” dice l’ingegnere “Vedo che in Scozia le pecore sono tutte nere”. “Hmm…” replica il fisico “Possiamo solo dire che qualche pecora scozzese è nera”. “No!” conclude il matematico “Tutto quello che sappiamo è che esiste in Scozia almeno una pecora la cui parte superiore del corpo è di colore nero”
“Ah, ah” rise di cuore Takami-musubi, che poi aggiunse “Lei, in quanto fisico teorico, sarà di sicuro abituato a pretendere, nelle relazioni che legge o scrive, una esposizione improntata all’accuratezza ed al rigore propri della matematica”
“Sì, certo. Siamo una specie di trait d’union tra fisica e matematica, tra la brillante intuizione e la stringente deduzione”
Dopo queste parole, e mentre l’aereo procedeva verso ovest a 800 chilometri orari, i due si fecero silenziosi, e poco dopo Takami-musubi si appisolò.
Ma solo per pochi minuti.
Al risveglio vide che il suo compagno di viaggio aveva scarabocchiato sul suo taccuino strani ghirigori che attrassero la sua attenzione e suscitarono la sua curiosità.
“Cosa disegna, professore?”
“Ah, questi? Sono diagrammi di Feynman”
“Feynman?”
“Sì. Richard Feynman era un fisico statunitense che ha vinto il premio Nobel 1965 insieme a Julian Schwinger e a un vostro connazionale, Sin-Itiro Tomonaga, per il suo lavoro fondamentale sulla elettrodinamica quantistica, l’argomento al centro appunto del convegno a cui ci stiamo recando”
“Non so nulla di… come si chiama? Ah… sì, elettrodinamica quantistica”
“Si consoli, non è il solo. Comunque Feynman è stato uno dei più brillanti scienziati del ventesimo secolo, un’autentica miscela esplosiva di genio, anticonformismo e carisma
Ha formulato un nuovo approccio per riformulare la meccanica quantistica, ha partecipato al progetto Manhattan sulla bomba atomica, suonava benissimo il tamburo bongo ed era bravissimo nello scassinare casseforti, mitiche sono le sue lezioni di fisica al Caltech a Pasadena, si è dedicato addirittura alla biologia e ha delineato un nuovo campo scientifico, quello delle nanotecnologie.
E mi sono dimenticato di sicuro qualcosa. Ci ha lasciato un ricordo indelebile e un’enorme eredità: quello che sapeva e, soprattutto, il modo unico in cui lo sapeva”
“Accipicchia!”
“Già, un vero mago della fisica. I suoi diagrammi, molto usati dai teorici, consentono di semplificare i calcoli. Ad esempio, vede quello che ho disegnato e ha attirato la sua attenzione?
Descrive l’annichilazione di una coppia particella – antiparticella con la successiva creazione di un’altra coppia di questo tipo.
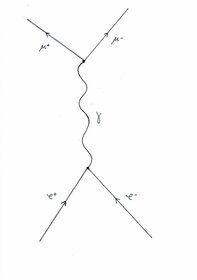
Il passare del tempo si può leggere dal basso verso l’alto. Abbiamo un elettrone e la sua antiparticella, il positrone, che si avvicinano fino a scontrarsi e annullarsi l’un l’altro. Viene così creato un raggio gamma, cioè un fotone di luce di altissima energia, che poi a sua volta dà origine ad una coppia muone – antimuone. Il muone è una specie di cugino dell’elettrone, in tutto simile ad esso ma più pesante.
Oppure, guardi: quello che sto disegnando adesso…
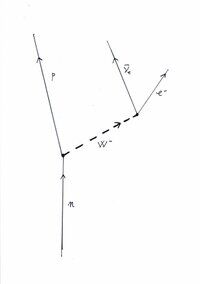
ci fa vedere invece il decadimento beta, cioè come un neutrone, quando non è legato nel nucleo atomico, muore dopo circa un quarto d’ora dalla nascita trasformandosi in un protone e dando origine anche ad un elettrone e un antineutrino. Avrà sentito parlare della bomba N, la bomba a neutroni; bene, si basa su questo decadimento. Con la linea tratteggiata è indicato un bosone W, particella molto pesante che prende parte a questo processo solo come particella virtuale”
“Virtuale?”
“Sì. E’ una cosa quasi incredibile. In base alla meccanica dei quanti sono possibili processi, che durano tempi brevissimi, nei quali l’energia non si conserva: è come se la Natura potesse prendere in prestito dell’energia extra a patto di restituirla dopo poco tempo. Più grande è l’energia in prestito e prima si deve restituire. E’ una conseguenza del principio di indeterminazione di Heisenberg. Abbiamo prove inconfutabili, solide come il marmo, che questi eventi capitano veramente!”
“Accipicchia, non lo sapevo”
“E questi processi avvengono continuamente nel vuoto. Coppie di particelle-antiparticelle compaiono dal nulla e dopo un tempo infinitesimo di nuovo sprofondano nel nulla, il vuoto è un oceano che pullula di questi processi virtuali. Gli effetti di questi processi devono essere tenuti in conto nei calcoli e si possono misurare. I risultati degli esperimenti concordano con i nostri calcoli in maniera spettacolosa.
Può succedere un po’ di tutto, sebbene con probabilità magari molto bassa. Per esempio, potrebbe capitare anche una cosa del genere
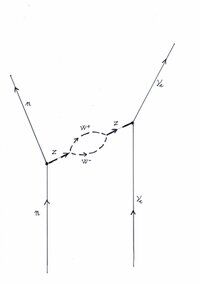
dove un neutrone interagisce addirittura con un neutrino, mediante lo scambio dei bosoni vettori intermedi W e Z. Vede?”
“Sì. Sono anche belli esteticamente, questi diagrammi”
“Le piacciono? Allora guardi questo!”
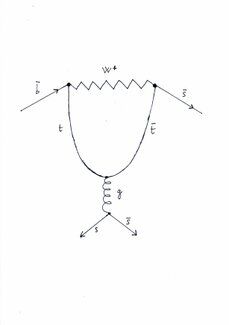
“Bello! Stranissimo”
“Già. Qui sono implicati i quark di tipo b,t,ed s. Ed anche, oltre al bosone W, un gluone, una particella che funge da colla nucleare dentro i protoni o i neutroni. Sa come è stato battezzato questo diagramma?”
“Beh… certo che no”
“Ora glielo racconto: due fisici entrano in un bar, ordinano da bere e iniziano una partita a freccette.
Fanno una scommessa: chi perde utilizzerà la parola pinguino nel suo prossimo articolo scientifico.
No, non è una barzelletta, è il motivo per cui nel 1977 in fisica delle particelle divenne d’uso comune il diagramma del pinguino, introdotto per la prima volta da John Ellis, lo scienziato del C.E.R.N. che perse la scommessa.
Infatti pochi giorni dopo Ellis, che stava lavorando con alcuni colleghi sulle proprietà del quark b, il quark bottom da poco scoperto, si accorse che esaminando il decadimento di un quark bottom in un quark strange, un altro tipo di quark, era necessario considerare anche quel diagramma, che somigliava abbastanza ad un pinguino.
Non gli parve vero di poter usare la parola pinguino nell’articolo che scrisse, per poter tener fede alla scommessa!
Ecco perché quel diagramma si chiama diagramma del pinguino, somiglia infatti ad un pinguino”
“Lei dice che ha le fattezze di un pinguino?” “Non riesce a vederlo? Chiuda gli occhi e si concentri”
“Uhmm… va bene” E Takami-musubi chiuse gli occhi e pensò al diagramma.
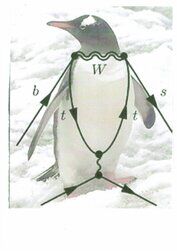
“Ah, sì, ora lo vedo. Ha proprio ragione! Sembra ad un pennuto polare”
“Già. Bello, no? E le dicevo che nei nostri calcoli di elettrodinamica quantistica dobbiamo tener conto di tutti i modi in cui queste particelle, reali o virtuali che siano, interagiscono l’un l’altra. Nel congresso di Itsukushima io farò un intervento in cui parlerò di alcuni particolari tipi di diagrammi di Feynman dei quali sono un esperto, i cosiddetti diagrammi tadpole, dove una linea congiunge un vertice con se stesso”
“Tadpole?”
“Sì, è lo stato di larva nel ciclo vitale di un anfibio, in particolare di rane o rospi”
“Ah, un girino, insomma”
“Esattamente. Un girino”
“Certo che ne avete di fantasia! Un pinguino e un girino. Non mi stupirei se in futuro nei vostri disegni di meccanica quantistica dovessero comparire altri animali, o magari specie vegetali”
A queste parole Coleman sorrise, girando contemporaneamente la tasta verso l’oblò.
“A proposito di vegetali, guardi laggiù, Takami, quanti begli alberi in fiore!”
“Sì, stiamo sorvolando la zona nei pressi di Nagoya. Qui il territorio è pieno di piantagioni di alberi da frutta, di questi tempi in piena fioritura”
“Che alberi sono quelli là proprio sotto di noi, ciliegi?”
“No. E’ ben vero che il Giappone è famoso per i suoi alberi di ciliegio, che sono quasi un simbolo della nazione, ma quelle sono piante di mandorlo, anche se i loro fiori, ad un occhio non esperto, potrebbero essere scambiati per quelli di ciliegio”
“E’ lei è un esperto di giardinaggio, vero? Almeno quanto io lo sono di diagrammi di Feynman, ho indovinato?”
“Sì, nel mio giardino curo, come hobby, piante di ciliegio e mandorlo. Ma possiedo anche alberi di pesco e altri arbusti”
“Capisco. Quanti sono!! Guardi”
“Sì. Qui da noi le piantagioni sono tutte di forma rettangolare, con un certo numero di file, ognuna rigorosamente composta da una dozzina di piante”
“Ah, vediamo quante file ci sono… una, due, tre…” e il professor Coleman si fermò solo dopo essere giunto al numero 32.
Immediatamente dopo chiuse gli occhi e la sua mente moltiplicò fulmineamente 12 per 30, aggiungendoci poi due dozzine, ottenendo come risultato 384.
Quando riaprì gli occhi vide che Takami aveva tracciato delle linee su di un foglietto.
“Cosa sta disegnando, Takami?” chiese Coleman, incuriosito.
“Oh, sto solo calcolando quanti mandorli ci sono”
“Eh?”
“Sì, sto solo facendo una moltiplicazione”
“Una moltiplicazione? E in che modo?”
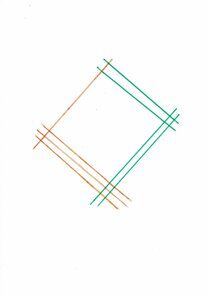
“Come la facciamo noi giapponesi. In questo caso dobbiamo moltiplicare 12 per 32.
Quindi abbiamo una decina e due unità: incominciamo a tracciare una linea, che rappresenta la decina, a sinistra in arancione dal basso in alto.
Poi a destra tracciamo due linee, le due unità, che qui io ho fatto in verde.

Subito dopo passiamo al numero 32, tre decine e due unità. In basso a sinistra rappresentiamo in arancione le tre decine, tracciando tre linee; e a destra in alto disegniamo le due linee verdi delle unità. Abbiamo finito.
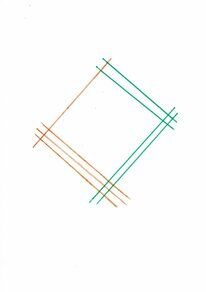
Ora possiamo leggere il risultato, contando i punti di intersezione tra le linee rette. A sinistra abbiamo 3 punti, e queste sono le centinaia, al centro 2 punti sopra e 6 sotto, per un totale di 8, e queste sono le decine, e infine a destra 4 punti, quelli delle unità. Tre centinaia, otto decine e quattro unità, il risultato dunque è 384 mandorli. E’ molto semplice”
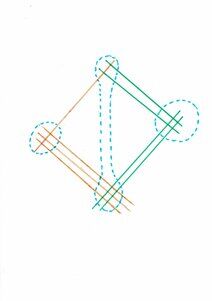
“Bellissimo: non avevo mai visto niente del genere. E 384 è proprio il risultato esatto”
“Certo che è esatto, sono secoli che in Giappone facciamo così le moltiplicazioni”
Coleman chiuse un attimo gli occhi e poi disse “Sì, ho capito perché funziona. Che bel viaggio è stato questo: lei ha imparato qualcosa dei diagrammi di Feynman e io come si esegue una moltiplicazione giapponese!”
Mentre Coleman finiva questa frase, ai due si avvicinò la graziosa hostess che li guardò dicendo:
“Desiderate qualcosa da mangiare, o da bere?”
“Io sto bene così, grazie” le rispose Takami-musubi.
“Io invece mangerei volentieri qualcosa, cosa avete?” chiese Coleman.
“Da mangiare abbiamo solo frutta secca: noci oppure mandorle”
Coleman si voltò prima verso il suo accompagnatore, che gli sorrise intuendo quello che lui avrebbe detto, e poi verso la ragazza dicendole: “Penso che in questo frangente le mandorle siano decisamente le più appropriate: me ne dia pure una decina, grazie!”
NOTTURNO
Per miliardi di anni, la Terra è stata silenziosa. Poi gli animali hanno iniziato a fare baccano.
Sì, dopo eoni nei quali il pianeta ascoltò soltanto le voci della pioggia, del vento e delle onde, inaspettatamente comparve … il frastuono della vita!
Sul limitare del bosco, ore venti della sera.
Il gracidio di una rana, l’ululato del lupo, lo zillare di una cavalletta. Frastuono.
Frastuono? Maldestro rumore che disturba o musica che rompe il silenzio?
Una rana che tenta di accordare le sue note al tintinnio della debole pioggia che lava le foglie; un giovane lupo che cerca di comunicare alla luna la propria esistenza; una cavalletta che vuole gridare il suo amore per il suo compagno. Il vento, intanto, effettua uno slalom tra gli alti alberi, accarezzando i larici e sfiorando faggi e pioppi. Un grosso alce calpesta, correndo, l’erba che cresce.
Nel sottobosco, brughi e ciclamini osservano attenti una lontra che guida, premurosa, i suoi piccoli al sicuro verso la tana. Le gocce donate dal cielo riflettono la moltitudine dei fusti agghindati da splendidi rami.
Interno del bosco, verso mezzanotte.
Il soffio del barbagianni, il sibilo dei serpenti e un furetto che potpotta. Fracasso.
Fracasso? Stonata rapsodia o sintonia di voci che accompagnano il silenzio?
La pioggia si placa addormentandosi, la luna ha vinto la battaglia: ormai si staglia nel cielo sempre più terso. Il saggio barbagianni si annoia, due serpenti intrecciano amorosi sensi, un furbetto furetto veloce si nasconde tra un frassino alto 20 metri e un tiglio vecchio di 500 anni.
Le quercie, gli aceri e gli olmi respirano quieti la fredda aria della notte. Un biacco invece soffia in direzione di un pino, mentre da questo un grappolo di pinoli, mosso dal vento, atterra sul suolo ornato da biancospini e gerani. Un pipistrello è in agguato.
Il lago al centro del bosco, le quattro della notte.
Il gufo che bubola, un orso che ruglia, lo squittìo dello scoiattolo. Rumore.
Rumore? Clamore disordinato o perfetta disposizione di note?
Il gufo è attento, all’erta, appollaiato su di un enorme castagno. L’orso passeggia indispettito, calpestando le clematidi e i ligustri, furente verso il mondo intero. Un giovane scoiattolo, atterrito dal plantigrado, si lamenta senza tregua mentre un ghiro annusa incuriosito un riccio chiuso su se stesso.
Sullo sfondo, indolenti, stanno robinie, betulle ed ontani intenti a succhiare dal’umido terreno linfa vitale.
Onde sonore trasportano la voce di un tordo che gruga. Più in là, ancora più in là, un alacre castoro si tuffa nelle nere acque, con un tonfo. Un pettirosso chioccola lamentandosi di una zanzara che zufola e ronza.
Voci nella notte: una arcana bellezza.
Un nuovo giorno si sveglia, le sei del mattino.
Un allocco che bubola, il trillo dell’allodola, una tortora che tuba. Fragore.
Puro e semplice fastidio od orchestra sapientemente accordata?
Il sole dà il cambio alla luna. Un’esplosione di luce.
E una esplosione di voci: la risata del picchio verde, un cinghiale che grufola, il bramito di un cervo e il gorgheggio dell’usignolo, lo zirlo del tordo e il gracchiare del corvo, un capriolo che rantega e una volpe che guaiola, il bombire dell’ape e il frinire delle cicale, il fischio della marmotta e della poiana, un’altra volpe che gannisce, un gorgheggio di una capinera e il gracchio della cornacchia, il chioccolio di un piccolo merlo insieme allo stridio della gazza.
Si desta la foresta, dove di giorno c’è posto per alcune cose e di notte c’è posto per altre, ma dove per la bruttura non c’è posto né di giorno né di notte.
Dalle profondità del bosco, accompagnati dallo stormire delle foglie, i timballi degli insetti, all’unisono con le laringi dei mammiferi e le siringi degli uccelli, danno vita a questo concerto mattutino, a questa sinfonia concepita unicamente per annunciare a tutti gli astri del cosmo che la Terra brulica di vita, che la Terra è bellissima, di una bellezza suprema, di una bellezza sublime!
Per qualche miliardo di anni... silenzio, solo scrosciar di pioggia e rombi di temporali.
Poi la musica della vita: qualche miliardo di anni, giusto il tempo di accordare gli strumenti.


